Note
Go to the end to download the full example code
1. Basic Usage Guide¶
pymer4 comes with sample data for testing purposes which we’ll utilize for most of the tutorials.
This sample data has:
Two kinds of dependent variables: DV (continuous), DV_l (dichotomous)
Three kinds of independent variables: IV1 (continuous), IV2 (continuous), IV3 (categorical)
One grouping variable for multi-level modeling: Group.
Let’s check it out below:
# import some basic libraries
import os
import pandas as pd
# import utility function for sample data path
from pymer4.utils import get_resource_path
# Load and checkout sample data
df = pd.read_csv(os.path.join(get_resource_path(), "sample_data.csv"))
print(df.head())
Group IV1 DV_l DV IV2 IV3
0 1 20.0 0 7.936508 4.563492 0.5
1 1 20.0 0 15.277778 0.000000 1.0
2 1 20.0 1 0.000000 0.000000 1.5
3 1 20.0 1 9.523810 0.000000 0.5
4 1 12.5 0 0.000000 0.000000 1.0
Standard regression models¶
Fitting a standard regression model is accomplished using the Lm model class in pymer4. All we need to do is initialize a model with a formula, some data, and call its .fit() method.
By default the output of .fit() has been formated to be a blend of summary() in R and .summary() from statsmodels. This includes metadata about the model, data, and overall fit as well as estimates and inference results of model terms.
# Import the linear regression model class
from pymer4.models import Lm
# Initialize model using 2 predictors and sample data
model = Lm("DV ~ IV1 + IV2", data=df)
# Fit it
print(model.fit())
Formula: DV~IV1+IV2
Family: gaussian Estimator: OLS
Std-errors: non-robust CIs: standard 95% Inference: parametric
Number of observations: 564 R^2: 0.512 R^2_adj: 0.510
Log-likelihood: -2527.681 AIC: 5061.363 BIC: 5074.368
Fixed effects:
Estimate 2.5_ci 97.5_ci SE DF T-stat P-val Sig
Intercept 1.657 -4.107 7.422 2.935 561 0.565 0.573
IV1 0.334 -0.023 0.690 0.181 561 1.839 0.066 .
IV2 0.747 0.686 0.807 0.031 561 24.158 0.000 ***
All information about the model as well as data, residuals, estimated coefficients, etc are saved as attributes and can be accessed like this:
# Print model AIC
print(model.AIC)
5061.3629635837815
# Look at residuals (just the first 10)
print(model.residuals[:10])
[-3.79994762 6.94860187 -8.32917613 1.19463387 -5.8271851 -6.88457421
0.40673658 9.77173122 -7.33135842 -7.37107236]
A copy of the dataframe used to estimate the model with added columns for residuals and fits are are available at model.data. Residuals and fits can also be directly accessed using model.residuals and model.fits respectively
# Look at model data
print(model.data.head())
Group IV1 DV_l DV IV2 IV3 fits residuals
0 1 20.0 0 7.936508 4.563492 0.5 11.736456 -3.799948
1 1 20.0 0 15.277778 0.000000 1.0 8.329176 6.948602
2 1 20.0 1 0.000000 0.000000 1.5 8.329176 -8.329176
3 1 20.0 1 9.523810 0.000000 0.5 8.329176 1.194634
4 1 12.5 0 0.000000 0.000000 1.0 5.827185 -5.827185
This makes it easy to assess overall model fit visually, for example using seaborn
# import dataviz
import seaborn as sns
# plot model predicted values against true values
sns.regplot(x="fits", y="DV", data=model.data, fit_reg=True)

<Axes: xlabel='fits', ylabel='DV'>
Robust and WLS estimation¶
Lm models can also perform inference using robust-standard errors or perform weight-least-squares (experimental feature) for models with categorical predictors (equivalent to Welch’s t-test).
# Refit previous model using robust standard errors
print(model.fit(robust="hc1"))
Formula: DV~IV1+IV2
Family: gaussian Estimator: OLS
Std-errors: robust (hc1) CIs: standard 95% Inference: parametric
Number of observations: 564 R^2: 0.512 R^2_adj: 0.510
Log-likelihood: -2527.681 AIC: 5061.363 BIC: 5074.368
Fixed effects:
Estimate 2.5_ci 97.5_ci SE DF T-stat P-val Sig
Intercept 1.657 -3.429 6.744 2.590 561 0.640 0.522
IV1 0.334 -0.026 0.693 0.183 561 1.823 0.069 .
IV2 0.747 0.678 0.815 0.035 561 21.444 0.000 ***
# Since WLS is only supported with 2 groups for now, filter the data first
df_two_groups = df.query("IV3 in [0.5, 1.0]").reset_index(drop=True)
# Fit new a model using a categorical predictor with unequal variances (WLS)
model = Lm("DV ~ IV3", data=df_two_groups)
print(model.fit(weights="IV3"))
Formula: DV~IV3
Family: gaussian Estimator: WLS
Std-errors: non-robust CIs: standard 95% Inference: parametric
Number of observations: 376 R^2: 0.999 R^2_adj: 0.999
Log-likelihood: -532.518 AIC: 1069.036 BIC: 1076.896
Fixed effects:
Estimate 2.5_ci 97.5_ci SE DF T-stat P-val Sig
Intercept 45.647 35.787 55.507 5.015 373.483 9.103 0.000 ***
IV3 -2.926 -15.261 9.410 6.273 373.483 -0.466 0.641
Multi-level models¶
Fitting a multi-level model works similarly and actually just calls lmer or glmer in R behind the scenes. The corresponding output is also formatted to be very similar to output of summary() in R.
# Import the lmm model class
from pymer4.models import Lmer
# Initialize model instance using 1 predictor with random intercepts and slopes
model = Lmer("DV ~ IV2 + (IV2|Group)", data=df)
# Fit it
print(model.fit())
Model failed to converge with max|grad| = 0.00358015 (tol = 0.002, component 1)
Linear mixed model fit by REML [’lmerMod’]
Formula: DV~IV2+(IV2|Group)
Family: gaussian Inference: parametric
Number of observations: 564 Groups: {'Group': 47.0}
Log-likelihood: -2249.281 AIC: 4510.562
Random effects:
Name Var Std
Group (Intercept) 203.390 14.261
Group IV2 0.136 0.369
Residual 121.537 11.024
IV1 IV2 Corr
Group (Intercept) IV2 -0.585
Fixed effects:
Estimate 2.5_ci 97.5_ci SE DF T-stat P-val Sig
(Intercept) 10.300 4.806 15.795 2.804 20.183 3.674 0.001 **
IV2 0.682 0.556 0.808 0.064 42.402 10.599 0.000 ***
Similar to Lm models, Lmer models save details in model attributes and have additional methods that can be called using the same syntax as described above.
# Get population level coefficients
print(model.coefs)
Estimate 2.5_ci 97.5_ci ... T-stat P-val Sig
(Intercept) 10.300430 4.805524 15.795335 ... 3.674034 1.487605e-03 **
IV2 0.682128 0.555987 0.808268 ... 10.598847 1.706855e-13 ***
[2 rows x 8 columns]
# Get group level coefficients (just the first 5)
# Each row here is a unique intercept and slope
# which vary because we parameterized our rfx that way above
print(model.fixef.head(5))
(Intercept) IV2
1 4.482095 0.885138
2 17.991023 0.622143
3 8.706144 0.838055
4 10.143487 0.865341
5 10.071328 0.182101
# Get group level deviates from population level coefficients (i.e. rfx)
print(model.ranef.head(5))
X.Intercept. IV2
1 -5.818335 0.203011
2 7.690593 -0.059985
3 -1.594286 0.155927
4 -0.156943 0.183213
5 -0.229102 -0.500026
Lmer models also have some basic plotting abilities that Lm models do not
# Visualize coefficients with group/cluster fits overlaid ("forest plot")
model.plot_summary()

<Axes: xlabel='Estimate'>
Plot coefficients for each group/cluster as separate regressions
model.plot("IV2", plot_ci=True, ylabel="predicted DV")
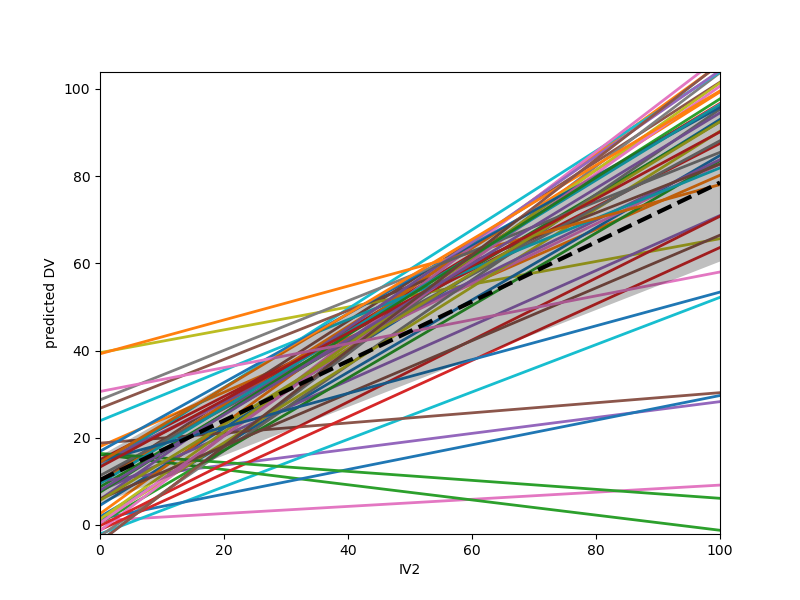
<Axes: xlabel='IV2', ylabel='predicted DV'>
Because Lmer models rely on R, they have also some extra arguments to the .fit() method for controlling things like optimizer behavior, as well as additional methods such for post-hoc tests and ANOVAs. See tutorial 2 for information about this functionality.
Two-stage summary statistics models¶
Fitting Lm2 models are also very similar
# Import the lm2 model class
from pymer4.models import Lm2
# This time we use the 'group' argument when initializing the model
model = Lm2("DV ~ IV2", group="Group", data=df)
# Fit it
print(model.fit())
/home/runner/work/pymer4/pymer4/pymer4/stats.py:657: RuntimeWarning: invalid value encountered in scalar divide
return 1 - (rss / tss)
Formula: DV~IV2
Family: gaussian
Std-errors: non-robust CIs: standard 95% Inference: parametric
Number of observations: 564 Groups: {'Group': 47}
Fixed effects:
Estimate 2.5_ci 97.5_ci SE DF T-stat P-val Sig
Intercept 14.240 4.891 23.589 4.644 46 3.066 0.004 **
IV2 0.614 0.445 0.782 0.084 46 7.340 0.000 ***
Like Lmer models, Lm2 models also store group/cluster level estimates and have some basic plotting functionality
# Get group level coefficients, just the first 5
print(model.fixef.head(5))
Intercept IV2
Group
1 3.039903 1.781832
2 23.388350 0.524852
3 4.904321 0.919913
4 23.304669 0.719425
5 18.378387 -0.256136
# Visualize coefficients with group/cluster fits overlaid ("forest plot")
model.plot_summary()
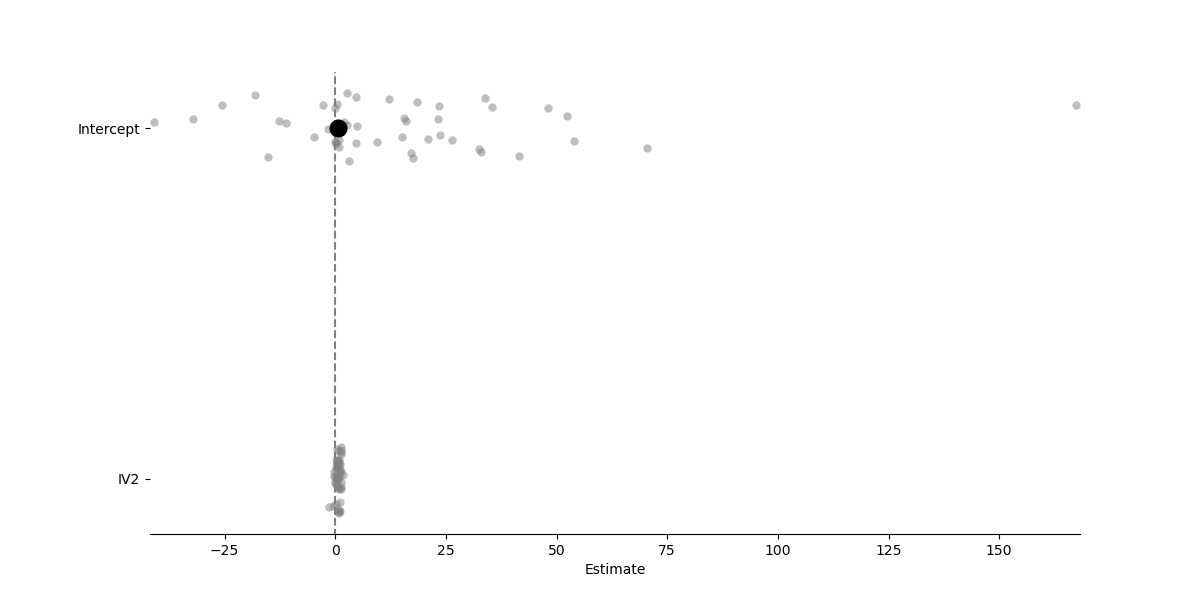
<Axes: xlabel='Estimate'>
Model Persistence¶
All pymer4 models can be saved and loaded from disk. Doing so will persist all model attributes and data i.e. anything accessible with the ‘.’ syntax. Models are saved and loaded using Joblib Therefore all filenames must end with .joblib. For Lmer models, an additional file ending in .rds will be saved in the same directory as the HDF5 file. This is the R model object readable in R using readRDS.
Prior to version 0.8.1 models were saved to HDF5 files using deepdish but this library is no longer maintained. If you have old models saved as .h5 or .hdf5 files you should use the same version of pymer4 that you used to estimate those models.
To persist models you can use the dedicated save_model and load_model functions from the pymer4.io module
# Import functions
from pymer4.io import save_model, load_model
# Save the Lm2 model above
save_model(model, "mymodel.joblib")
# Load it back up
model = load_model("mymodel.joblib")
# Check that it looks the same
print(model)
pymer4.models.Lm2(fitted=True, formula=DV~IV2, family=gaussian, group=Group)
Wrap Up¶
This was a quick overview of the 3 major model classes in pymer4. However, it’s highly recommended to check out the API to see all the features and options that each model class has including things like permutation-based inference (Lm and Lm2 models) and fine-grain control of optimizer and tolerance settings (Lmer models).